The Quotable Astroboy

October 27, 2008UncategorizedA Threeheaded Monkey with a Typewriter

In all my time on Earth the following two episodes of Astroboy is by far the funniest thing I have ever seen:

Astroboy – The Greatest Robot in the World (1/6) (I trust people to find the remaining 5 videos on their own.)

Just give it time to start and I promise you that you will watch it to the end. The dialogue is without equal. “You can’t stop me! NO ONE can stop me!”

I don’t want to give too much away but in the end people are reconciled and an important lesson is learned.

Center for Ultrafast Intense Laser Science

March 23, 2008UncategorizedA Threeheaded Monkey with a Typewriter

Working at a center like that would be enough to finally convince me to have business cards made.

PhD Defences

January 27, 2008Uncategorizedthetcs

Mr. Scientist: I can’t help worrying a little bit about the defence.
Mr. Monkey: Everyone does.
Mr. Monkey: Do you have specific worries?
Mr. Scientist: No, not really.
Mr. Monkey: Then you will do fine.
Mr. Scientist: I just can’t shake the fear that some day, I will be exposed as a dilettante.
Mr. Monkey: I had that feeling too but the question session at my defense basically went like this:
Mr. Monkey: Adviser: “Does anybody have any questions?”
Mr. Monkey: Referees: *cricket sounds*
Mr. Monkey: Adviser: “Well, then … I will ask some.”
Mr. Scientist: !
Mr. Monkey: I am glad I got my degree but I would have liked some more enthusiasm from the committee.
Mr. Monkey: Or at least an indication that they had leafed through my dissertation.
Mr. Scientist: I got a preliminary report from the committee which actually contains astute if not quite deep comments.
Mr. Monkey: “Your dissertation has a front page, I see.”

Administration

December 13, 2007Uncategorizedthetcs

2My research is temporarily impeded by my compulsory filling in of a 96-question questionnaire on the quality of the PhD-education at my alma mater. As always, I’m thrilled to oblige the PhD study board.

Arriving at the question “Anything you want to add about study plans and half-year reports?” I wonder what to write. Having discussed this particular issue with members of the study board on numerous occasions, I’m sure they are familiar with my position. On the other hand, they are specifically asking if I “want to add anything”. I can’t help myself.

Pointless inane bureaucracy.

Suppose, for the sake of argument, that my supervisor could not guide me to a degree were it not for the study board’s valiant insistence that I concoct a study plan. I am dismayed and insulted that you return my study plan — clearly having read only the timetable — and order under threat of exmatriculation that it be changed and resubmitted.

Now, normally when faced with such presumptuous arrogance and paper-pushing stupidity, I would suffer it silently, but since you so foolishly solicit my opinion, here it is: In the case of study plans and half-year reports, the study board has descended into the mind-numbing bureaucracy of well-meaning nitwits.

I’ll be in 4C07 if you have any questions.

Noether’s Theorem: Sounds Like a Star Trek Episode!

August 28, 2007UncategorizedA Threeheaded Monkey with a Typewriter

Captain’s log, stardate 435920.6: It’s another Sunday afternoon in the Dwingeloo galaxy. And it’s time for tea.

You may not be in the Dwingeloo galaxy. You may be on Earth. Perhaps even in a time zone that does not count the time of this posting as Sunday. I … well … I have been busy. And it’s very hot. And my horoscope has been unfavourable. Also, Godzilla ate my homework. I was walking down the street when Godzilla just snatched it out of my hand and ate it. It’s ridiculous, really. There is never a power ranger in sight when you need one. And at other times you just can’t seem to shake them. My point is: I have really sound reasons for being behind my posting schedule.

Noether’s Theorem

I can’t really claim to understand Noether’s Theorem to the extent that I would like but ignorance of the subject at hand will not stop me as I also told the nurse who was skeptical of my ability to perform brain surgery last Wednesday.

To business! Imagine that you have chosen variables to describe your physical situation $q_1, \ldots, q_n$ . These could be angles, positions and basically anything that has tickled your fancy. We will write $q$ for the collection of variables and $\dot{q}$ for the corresponding collection of time derivatives. You then write your Lagrangian $L(q, \dot{q}) = T - U$ where $T$ denotes kinetic energy and $U$ denotes potential energy. You will recall – or out of politeness at least pretend to recall – that the motion of the system is completely determined by the Lagrange equations:

$\frac{d}{dt} \frac{\partial L}{\partial \dot{q}_i} - \frac{\partial L}{\partial q_i} = 0 , \quad \quad i = 1, \ldots, n .$

Now, imagine that there is some kind of continuous transformation of the system that leaves the Lagrangian invariant. An example could be translation. Say the function $h_s$ takes the variables $q_1, \ldots, q_n$ and effects a translation of $s$ meters in a fixed direction. Obviously the function $h$ should satisfy $h_r \circ h_s = h_{r+s}$ and it needs to be “nice” as we will need to differentiate it later. That the Lagrangian is invariant under the transformation means that

$L(q(t),\dot{q}(t)) = L(h_s(q(t)), \frac{d h_s(q(t))}{dt})$ .

Noether’s Theorem states that whenever we have a family of transformations $h_s$ that leave the Lagrangian invariant, there exists a corresponding conserved quantity. This conserved quantity is

$I = \sum_{i=1}^n \frac{\partial L}{\partial \dot{q}_i} \frac{d h_s(q_i)}{ds} |_{s=0}$ .

That is not a very enlightening formula, I must admit. It’s a relatively simple proof to show that the quantity $I$ is conserved but less simple to convey in words what it means. Perhaps more enlightening would be to consider some concrete transformations.

Arguably the most famous application of Noether’s Theorem is that invariance under time translations (a case I ruled out above by not including time in the Lagrangian) implies conservation of energy. Invariance under translations imply conservation of momentum $P = \sum_i m_i v_i$ where $v_i$ is the velocity vector of the ith particle. Likewise well-known is that invariance under rotations imply conservation of angular momentum; the thing that keeps your spinning top and ice skaters from keeling over.

It is a general assumption about the universe that the physical laws are invariant under the above-mentioned transformations so we expect conservation of energy, momentum and angular momentum. Of course, these laws of conservation only hold as long as we make our system large enough. If, for instance, we were to perform experiments on Earth but didn’t include Earth itself in the system we considered, we would not have conservation of momentum amongst other things because of gravity. Horizontal momentum would still be preserved but gravity would spoil the fun for vertical momentum.

Because we seldom include the entire universe in our systems we might not have rotational or translational invariance but other kinds of invariances. Let’s say that you have chosen a system in such a way that it is invariant under movement in a spiral; I have no idea why you did this but let’s say that you did. In that case using Noether’s Theorem would reveal that your system had a conserved quantity which would be a mixture of momentum and angular momentum (along the axis you are madly spiralling about). Contrived examples aside, energy, momentum and angular momentum remain the standard conserved quantities for physical systems.

And thus we come to the end of this rather brief and yet still cluttered exposition. I’m sure we have all learned something. I for one have learned that WordPress is not the medium you should choose if you wish to include mathematical formulae. But goodbye from all of us. And by “us” I mean me and the jungle fowl:

Jungle fowl, sunset

Above: A jungle fowl stops one last time to look back before it rides into some orange stuff in the background that could very well be the sunset.

Lagrangian Mechanics and the Wonders They can Work on Your Lagrangian Car

August 20, 2007UncategorizedA Threeheaded Monkey with a Typewriter

Well, it’s a beautiful Sunday evening on Hawaii. There is a clear sky and the air is pleasantly warm. Anyway, for the second installment of antique mechanics, we turn to Lagrangian and Hamiltonian mechanics. The conversational choice for the hermit in spe.

Newtonian mechanics is all about solving equations of the form $F = ma$ . That sounds easy, you probably think, and most people would agree with you: Newtonian mechanics just lacks that satisfying, elitist feel of being inaccessible to the common person. Cue Lagrangian mechanics. But first two quick asides on notation and energy.

Notation
As before $x$ will denote position. We will imagine that we have N particles with positions $x_1, \ldots, x_N$ and respective masses $m_1, \ldots, m_N$ . We denote time derivatives with a cute dot on top and if $f$ is a scalar function dependent on the positions, $\frac{\partial f}{\partial x_i}$ denotes the gradient of $f$ with respect to $x_i$ . The letter “k” – even if appearing in the context of a word – will denote unconditional love beaming happily at you from the screen. Bear this in mind and reading this post will leave you sated with a warm, blissful feeling.

Energy

In many cases the force acting on the $i$ th particle, $F_i$ , can be expressed as the gradient $\frac{\partial U}{\partial x_i}$ for some scalar function $U = U(x_1, \ldots, x_N)$ called the potential energy. To make things nice a minus-sign is added. That is,

$\quad F_i = - \frac{\partial U}{\partial x_i}$ .

If one were in a quiet moment to differentiate $U$ with respect to time, one would find that

$\quad \frac{dU}{dt} = \frac{\partial U}{\partial x_1}\dot{x}_1 + \cdots + \frac{\partial U}{\partial x_N} \dot{x}_N$ .

Replacing the derivatives of $U$ with the corresponding forces, $\frac{\partial U}{\partial x_i} = - F_i = - m_i \ddot{x}_i$ , we find

$- \frac{dU}{dt} = m_1 \dot{x}_1 \ddot{x}_1 + \cdots + m_N \dot{x}_N \ddot{x}_N = \frac{d}{dt} \left( \frac{1}{2} m_1 \dot{x}_1^2 + \cdots + \frac{1}{2} m_N \dot{x}_N^2 \right).$

So, defining the kinetic energy of the $i$ th particle as $T_i = \frac{1}{2} m_i \dot{x}_i^2$ and the total kinetic energy, $T$ , as the sum of the $T_i$ ‘s, $T = \sum_i T_i,$ the total energy, defined as $E = T+U$ , is consequently constant.

Lagrangian Mechanics

The usual way of showing that Lagrangian mechanics and Newtonian mechanics are equivalent feels very much like trying to prove that Paris and London are connected by road by driving a car all the way from Vladivostok to Paris, stopping for a quick cappucino, and then continuing on to London. I will break tradition by starting the car in Paris but I will show pictures from the Vladivostok-Paris trip afterwards.

We assume in the following we are dealing with a system where the force is given by a potential energy as in the discussion above.

Now, Newton’s 2nd law can be written $F_i - m_i \ddot{x}_i = 0$ . Defining the Lagrangian $L = T - U$ and noting that $F_i = - \frac{\partial U}{\partial x_i} = \frac{\partial L}{\partial x_i}$ and that $m_i \ddot{x}_i = \frac{d}{dt} \frac{\partial}{\partial \dot{x}_i} (\frac{1}{2} m_i \dot{x}_i^2) = \frac{d}{dt} \frac{\partial L}{\partial \dot{x}_i}$ , we see that Newton’s 2nd law can be rewritten as

$\quad \frac{\partial L}{\partial x_i} - \frac{d}{dt} \frac{\partial L}{\partial \dot{x}_i} = 0, \quad \quad i =1, \ldots, N .$

And that is the Euler-Lagrange equations that define Lagrangian mechanics (for a special choice of variables). A simple rewrite of Newton’s 2nd law, a fancy French name and sim-sa-la-bim it has the air of something that will separate you from the rabble. But it gets even better!

So what was this Vladivostok-Paris trip I was talking about? Well, imagine that instead of the coordinates $x_1, \ldots, x_N$ (which is really $3N$ variables as each $x_i$ is a vector) you wish to use some other variables $q_1, \ldots, q_{3N}$ . As variables go, rather than using the positions, it is often easier to use angles, positions relative to other particles and whatnot to exploit symmetries and simplify expressions. If you do that it can be shown that the motion of the system is still described by the Euler-Lagrange equations of the following form:

$\frac{\partial L}{\partial q_i} - \frac{d}{dt} \frac{\partial L}{\partial \dot{q}_i} = 0, \quad \quad i =1, \ldots, 3N .$

This can be shown directly by mucking about with partial derivatives but there is a more elegant way in which the Euler-Lagrange equation is shown to have as solution the motion $t \mapsto x(t)$ for which the functional $t \mapsto \Phi(t) = \int_{t_0}^{t_1} L(x(t),\dot{x},t) dt$ is extremal (in a sense that a minimal regard for brevity stops me from going into). The important point to make here is that being “extremal” is independent of the variables chosen. And this independence of the choice of variables is exactly what the Vladivostok-Paris trip is about.

That the Euler-Lagrange equations describe the extremals of the functional $\Phi$ is called Hamilton’s form of the principle of least action. I find this naming convention very sad because not only is it not true that every extremal is a minimum, it also misses out on a perfect opportunity of appealing to today’s students by giving it the more correct and far cooler name of “Hamilton’s principle of extreme action!!!”

Hamiltonian Mechanics

While impromptu soliloquies on Lagrangian mechanics is sure to impress everyone at your local pub, it will earn you little more than a speedy exit from a more upscale bar. For the discerning audience you will have to turn to Hamiltonian mechanics.

The obscurity – and thus that comforting, superior feeling of flying 1st class – of Hamiltonian mechanics relies on the application of the Legendre transformation. The Legendre transformation is basically reparametrizing a function $f$ in terms of its slope. For a function $f : \mathbb{R} \rightarrow \mathbb{R}$ with $f'' > 0$ , the Legendre transformation of $f$ is

$F(p) = p x_p - f(x_p)$

where $x_p$ is the unique point satisfying $f'(x_p) = p$ . A funny exercise (in the sense that it is funny to watch people struggling with notation trying to do it) is to show that using the Legendre transformation twice brings you back to the original function.

In the following I will assume that the Lagrangian only depends on one single variable $q$ as well as it’s time derivative $\dot{q}$ and the time $t$ . That is, $L = L(q, \dot{q}, t)$ . Considering the Lagrangian as a function of $\dot{q}$ we can apply the Legendre transformation to obtain a new function,

$H(q,p,t) = p \dot{q}_p - L(q, \dot{q}_p,t)$

where the relationship between $p$ and $\dot{q}$ is given by $p = \frac{\partial L}{\partial \dot{q}}$ .

In Hamiltonian mechanics the motion of the system is given by the Hamiltonian equations:

$\dot{p} = - \frac{\partial H}{\partial q} \quad \text{and} \quad \dot{q} = \frac{\partial H}{\partial p}.$

Hamiltonian mechanics can be shown to be equivalent to Lagrangian mechanics and thus also to Newtonian mechanics simply by writing out the partial derivatives. You will not be surprised that I am not going to do that.

An important observation about the Hamiltonian is that if you were a bit careful in the choice of your variables, the Hamiltonian function $H$ is simply the total energy of the system. Since energy is generally a known function of the system, it is easy to write down the Hamiltonian and get on with the fun of differentiating.

Comments I should have worked into the above but didn’t

Lagrangian and Hamiltonian mechanics come about by rather simple rewrites of Newton’s 2nd law and so it is hardly to be expected that they bring very great revelations to the table. Within the framework of classical mechanics their main advantage lies in providing an easy way to solve problems. Anyone who has ever tried to find the motion of a system involving trolleys, balls and flying monkeys knows how tedious it can get writing all the forces, adding up, balancing out and then integrating. The Lagrangian and Hamiltonian functions are usually much simpler to write and the differential equations are only first order as compared to the 2nd order differential equation in the Newtonian case.
Another – and arguably more important – advantage to Lagrangian and Hamiltonian mechanics is that they are easier to generalize to quantum mechanics for instance than Newtonian mechanics. Not really easy, but easier.
Should you ever need it, you will be glad to know that Lagrangian mechanics provides an easy philosophical shutdown (I will trademark that term) of undergraduate physics students. Simply ask them what the physical interpretation of the Lagrangian and its being an extremal of the aforementioned functional $\Phi$ really is. If the student has had just two beers, I guarantee that you will hear no more from him. It’s the equivalent of pointing out a logical error in the guiding principles of the killer robot you face guarding the door to the Evil Plans and Holding Your Girlfriend Hostage R Us Corporation (LLC) or shouting “DO YOU HAVE FREE WILL?” into the cafeteria at the institute of philosophy.

Classical Mechanics and the Jungle Fowls of Doom

August 13, 2007UncategorizedA Threeheaded Monkey with a Typewriter

I have long been meaning to reread some things I should know well but don’t, so I finally thought that adding the pressure of having shouted out my intention of getting the reading done into the obscurity of the fog that is the internet would be that rocket-powered boost I so sorely need to get things done. My intention is to write three posts spread out over today and the following two Sundays about classical mechanics each with some kind of highlight of what I have read by then.

Newton’s Laws and How to Get a Reaction out of People by Hitting Them
Lagrangian Mechanics and the Wonders They Can Work on Your Lagrangian Car
Some Stuff Probably Involving Noether’s Theorem

“So what is in it for me,” I hear you cry while throwing rotten tomatoes from out of the fog. Well, if I don’t deliver I promise to buy a beer for any person bringing this failure up in conversation with me (only the first mention of my failure buys you a beer). Also, I promise to mention Jungle Fowls of Doom!!!

To keep it relatively short and to avoid boring you too much I will skirt casually over some things. Think of this as the kind of conversation you would have in a bar. You know, the kind where some drunken guy has maneuvered you into a corner and launched into a monotonous, barely comprehensible monologue devoid of meaning and humour. I hope you at least got a full beer. No? Well, too late.

Newton’s Laws and How to Get a Reaction out of People by Hitting Them

Despite classical mechanics being on the highschool curriculum I doubt many people know what Newton’s laws actually say as it seems to be a teaching tradition to (a) not explain their meaning to the students, and (b) otherwise be annoyingly vague. The main obscurity lies with Newton’s 2nd law which is usually presented as “Force equals mass times acceleration” (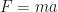 $F = ma$ ) with less explanation of the concept of “force” than one might pick up by a drunken viewing of Star Wars. “Force has to be determined experimentally,” you might be told if you inquire about it. Nevermind that you could write any random expression, declare it equal to Huffle-Muffle and claim that Huffle-Muffle had to be determined experimentally. But enough about my bitter, personal experiences disguised as generalities.

There are three issues to be addressed: What is the space-time? What are inertial systems? What happens in inertial systems?

Space-time
The underlying assumption of classical mechanics is that space-time can be modelled as $\mathbb{R} \times \mathbb{R}^3$ with the first coordinate being time. Well, actually the proper assumption is that it is a real 4-dimensional affine space, meaning it is basically like $\mathbb{R}^4$ except without a fixed origo. This is not a very strong assumption and is in fact broad enough to allow for a good deal of the theory of general relativity. Points in the space-time are called events to make them sound exciting.

The space-time is furthermore assumed to be equipped with a Galilean structure. Without going into details this means that for any two events there is a time difference and for simultaneous events (those with no time difference) there is a notion of distance.

Galilean transformations are defined as affine transformations (basically a linear mapping combined with a translation) of space-time that preserve the Galilean structure, i.e., that preserve intervals of time and distance between simultaneous events. It is easy to show – or at least would be if I had given precise definitions – that any Galilean transformation can be decomposed into (a) a uniform motion, (b) a translation, and (c) an orthogonal transformation of space (that is, reflections and rotations).

Inertial Systems
For the present purposes let’s say that two coordinate systems are Galileically equivalent (yes, I just made that term up) if they differ only by a Galilean transformation.

We assume in classical mechanics that there exists a Galileic equivalence class of coordinate systems such that any physical experiment will play out the same way in all the systems in the equivalence class. Such a class will be called a class of inertial systems and any coordinate system in such a class will – unsurprisingy – be called an inertial system.

It should be stressed that existence is the key here. Moreover, not all coordinate systems will be inertial. For instance, if you define an x-axis as straight along your nose, a y-axis along your outstretched left arm and a z-axis up through your head and you start spinning around, then you won’t be an inertial system. Sorry.

Newton’s Principle of Determinacy
For now we will consider systems of particles only. This is only an expository convenience and not a limitation of classical mechanics; by “integrating up” complex bodies can be described through the particle formalism.

The single most important assumption of classical mechanics is this:

The motion of n particles depends only on their initial positions and initial velocities.

This is essentially Newton’s 2nd law in a rough form. It’s hard to doubt this assumption as it is ingrained in us from early experience. One could of course imagine a more complex and exciting hypothetical world where the motion of a system would depend also on the initial accelerations or even higher derivatives but our world seems to make do with just positions and velocities. That’s the kind of crappy, low-quality world you get when God rushes through creation in six days. Thanks a lot, God.

Getting Around to Newton’s Equations
Again we will restrict ourselves to the N particle picture. We choose a coordinate system for our space-time and denote by $x_1, \ldots, x_N$ the positions of the particles. We write $\boldmath{x}$ for $(x_1, \ldots, x_N)$ .

The principle of determinacy above states that all motions of the system are determined by the initial positions and velocities of the particles. In particular, there must exist a function $F: \mathbb{R}^N \times \mathbb{R}^N \times \mathbb{R} \rightarrow \mathbb{R}^N$ such that

$\ddot{\boldmath{x}} = F(\boldmath{x}, \dot{\boldmath{x}}, t)$

By the usual existence and uniqueness of solutions to ordinary differential equations, the function 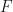$F$ along with the initial conditions uniquely determine the motions of the system.
The absence of ” inertial mass” in the equation is intentional. Defining inertial mass is another issue and one which I will skip.

Now, assuming that we didn’t choose our coordinate system all willy-nilly but were uncharacteristically careful and chose an inertial system, the definition of an inertial system entails that the function 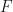$F$ must be invariant under Galilean transformations. The invariance under time translation implies that 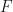$F$ does not depend on the time parameter $t$ in the equation above. Moreover, the invariance under spatial translations implies that 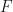$F$ does not depend directly on the positions but only on the relative positions. Invariance under uniform motion in turn implies that 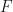$F$ does not depend directly upon the velocities but only on the relative velocities.

Consequently, we can rewrite our version of Newton’s 2nd law as

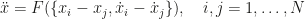
$\boldmath{ \ddot{x} = F(\{x_i - x_j, \dot{x}_i - \dot{x}_j \}) }, \quad i,j = 1, \ldots, N$

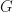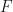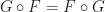We haven’t taken into account the invariance under orthogonal transformations in the above. Suffice it to say that if $G$ is a Galilean transformation then $F$ should satisfy (with abuse of notation) $G \circ F = F \circ G$ .

Some Final Comments
And thus, having arrived at Newton’s 2nd law our brief journey ends. I want to stress that the whole point of Newton’s 2nd law and the concept of force is what variables the force depends on. In its basic form Newton’s 2nd law simply says that initial positions and velocities determine all future motions of the system. No more.

Secondly I want to stress that being an inertial system is not (in a sense) an entirely intrinsic property of a coordinate system. Being inertial is the property that you cannot through experiments tell the given coordinate system apart from other coordinate systems that differ only by a Galilean transformations.

And thirdly, I wish to stress that Newton’s 2nd law in its basic form holds in all coordinate systems. The use of introducing inertial systems is that the invariance under Galilean transformations greatly simplify the function 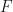$F$ .

Fourthly, and I should perhaps have mentioned this earlier, there are no truly inertial systems. A coordinate system fixed with respect to Earth is approximately inertial as long as you don’t venture to far away (don’t leave Earth). A coordinate system fixed with respect to the sun or the fixed stars is even more “nearly inertial”. At any rate it is an approximation and as with most things in physics it has a range of applicability that should not be exceeded.

Fifthly, if that is really what it is called, I want to mention jungle fowls of doom as I know that is what got you reading in the first place. So here: Jungle Fowls of Doom!!!

A Jungle Fowl of Doom stops in its tracks, suddenly realizing a division error in its calculations for the space shuttle launch.

Sushi on a stick

January 19, 2007UncategorizedA Threeheaded Monkey with a Typewriter

Have you ever spent an idle afternoon reclined in your favourite chair, languidly fingering a 512 Mb memory stick, wistfully observing it weave and wind between your fingers and thought to yourself, “I wish my memory stick looked like sushi”?

Of course you have.

Happily, the computer industry stands ready to cater to your culinary fantasies.

Sushi on a stick

And those allergic to fish are not left behind.

Hidden memory stick

It is not the bowl itself that is the memory stick; it is one of the meatballs. But which one, you wonder. Well, I hope you like pondering that particular question because if you buy that bowl it is the very one you will be asking yourself every single time you need your memory stick in the future.

Now, while an entire tray of sushi-like memory sticks is a sight sure to impress any visitor, it is admittedly not kind on the wallet. Thus, if you are on a budget you will be glad to know that a similar visual effect can be achieved simply by putting ordinary, actually edible food on your desk next to the computer and hiding your plain, old memory sticks in the drawer.

I have this great idea for a TV-show!

January 10, 2007UncategorizedA Threeheaded Monkey with a Typewriter

Have you ever struggled through any of Kierkegaards works and desperately wanted someone with whom to debate the interpretation? Well, bugger off, book-lover. You have come to the wrong place.

If on the other hand you have ever had what seemed to you to be a brilliant and novel idea for a TV-show but which was ridiculed by friends, lampooned by enemies, spurned by producers and urinated on by small forest animals, this post is for you!

Let’s for argument’s sake say that you are trying to pitch the idea of a televised duel to a producer. With pies. Done by two immobile duellants situated 1.5 meters from each other. Riding those useless rodeo fitness machines peddled by TV-Shop.Yes, you nod slowly to yourself with smug satisfaction while stroking the faint beginnings of a mustache, it is indeed a good idea. A great idea one might even say. Women will want you. Men will want to be you. You will stop receiving spam mail. People will stop crowding into the train while you are trying to exit. And Peter from the 5th grade will finally admit that Batman can beat Spiderman. The world is yours.

However, chances are that grim reality (once again) sees things in a different light and that you will (once again) face nigh universal castigation. But do not despair, nor listen to the horde of critics describing you alternately as an utter fool, a witless moron, and as the greatest threat ever to face the world’s gene pool. Instead merely add the words “Done by bikini-clad girls” to your proposal and *KAZAM* you have a well above average late-night show.

Ye olde YouTube-link

If you are a philistine with no YouTube-account, you can still see the video here:
Somewhere else on the net

the contemporary male

January 5, 2007Uncategorizedthetcs

In my daughters’ kindergarden, I rummage through the ‘forgotten-clothes’ bin, looking for a pair of red gloves. Just as I find them, another parent – a mother – passes by.

“Wow! You are looking through the ‘forgotten-clothes’ bin! Impressive! Very impressive!”
“Impressive?”
“My husband would never know our boys’ clothes from that of the other kids.”
“I am just looking for my daughter’s red gloves.”
“Yes! Impressive! My husband would never know our boys’ clothes from that of the other kids.”

I don’t know to what extent we are actually communicating. I hate that feeling; it’s far worse than simply not communicating.

“Well, …, thanks.”
“Don’t mention it. Bye!”

My masculinity thus confirmed, I fetch the kids, go home, start fixing dinner. My wife comes home from work.

“Hi honey”, I say, “Dinner’s ready shortly.”
“Good. Do you think we could start a chain of hotels in Eastern Europe?”

My somewhat career-minded wife is taking an MBA in her spare time. She has apparently been studying while riding the train home.

“I’d rather not. I found the red gloves, though.”

I point. She looks.

“Those aren’t ours; ours had frills on the bottom.”

The Theoretical Computer Scientist

Reconciling theory and practice since 2006

The Quotable Astroboy

Center for Ultrafast Intense Laser Science

PhD Defences

Administration

Noether’s Theorem: Sounds Like a Star Trek Episode!

Lagrangian Mechanics and the Wonders They can Work on Your Lagrangian Car

Classical Mechanics and the Jungle Fowls of Doom

Sushi on a stick

I have this great idea for a TV-show!

the contemporary male